0x01 自然数&整数

自然数Natural number

自然数是指用以计量事物的件数或表示事物次序的数，由0开始，标示为：
1，2，3，4，…，n，…

具体概念总结：

1. 自然数是一个无穷的集体
2. 自然数有有序性，无限性，分为偶数和奇数，合数和质数等
3. 自然数集是全体非负整数组成的集合，常用 N 来表示

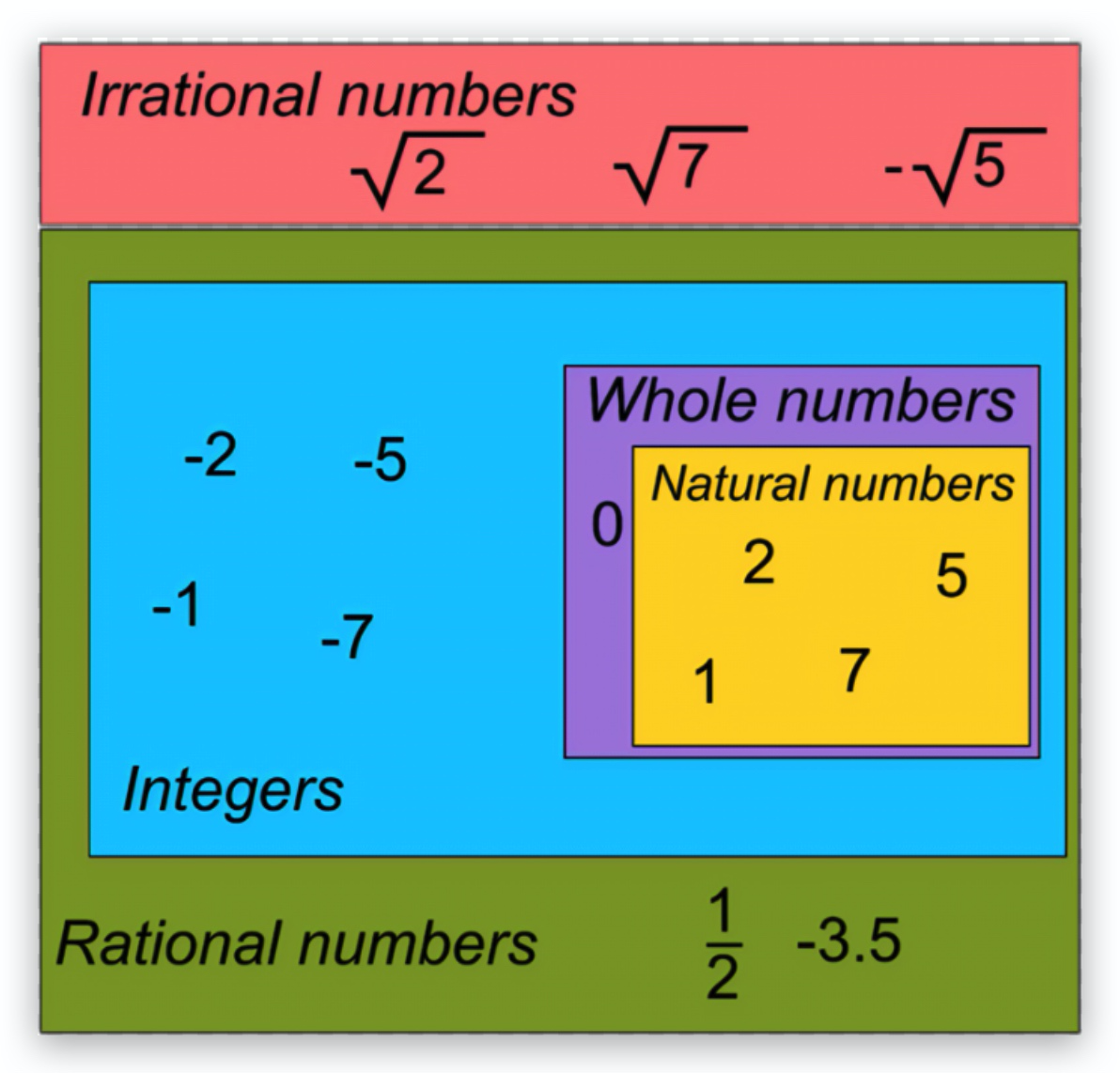
整数（integer）

整数是正整数、零、负整数的集合
-n，-2，-1，0，1，2，…，n，…

具体概念总结：

1. 整数的全体构成整数集，整数集是一个数环
2. 在整数系中，零和正整数统称为自然数
3. 整数也可分为奇数和偶数两类

整数加法和乘法的基本性质

初等数论中指出，在正整数集合中的加法运算“+”中，对任意的 a,b ∈ N，必有 x ∈ N 使得 x = a+b，称为a和b的和
但是在N中，对任意的 a,b ∈ N，不一定有x ∈ N，使得 a = b+x，也就是在N中不一定能作加法运算的逆运算 —— 减法运算“-”

在乘法集合中，可以作乘法运算“X”，但不一定满足乘法的逆运算 —— 除法运算

乘法运算满足：

大小关系

“＝”：等号
“≈”：近似符号
“≠”：不等号
“＞”：大于符号
“＜”：小于符号
“≥”：大于或等于符号（也可写作“≮”）
“≤”：小于或等于符号（也可写作“≯”）

性质：

1. 对任意的a,b,c ∈ Z，若 a≤b 且 b≤c，则a≤c
2. 对任意的a,b,c ∈ Z，若 a=b 且 b=c，则a=c
3. 对任意的a,b ∈ Z，对任意的c ∈ N，ab≤ac，则b≤c
4. 对任意的a,b ∈ Z，a≤b，则b≤a

0x02 自然数原理&归纳原理

如果S是N的一个子集

1. 1 ∈ S
2. n ∈ S，则 n+1 ∈ S
   那么 S = N

数学归纳原理

P(n) 是关于自然数 n 的一种性质或命题，如果：

1. n=1 时，P(1)成立
2. 由 P(n) 成立推导出 P(n+1) 成立
   那么 P(n) 对所有自然数n成立

最小自然数原理

T 是 N 的一个非空子集，那么必有 t0 ∈ T，使得任意 t ∈ T 存在 t0 ≤ t，则t0 是T的最小自然数

最大自然数原理

M 是 N 的一个非空子集，那么必有 m0 ∈ M，使得任意 m ∈ M 存在 m0 ≥ m，则m0 是T的最大自然数

第二种数学归纳法

P(n) 是关于自然数 n 的一种性质或命题，如果：

1. n=1 时，P(1)成立
2. 若 m>1，所有自然数 n<m，P(n)成立，则P(m)成立

抽屉原理

也称为鸽巢原理🐦（Pigeonhole principle）

桌上有十个苹果，要把这十个苹果放到九个抽屉里，无论怎样放，我们会发现至少会有一个抽屉里面放不少于两个苹果

也就是👇

“如果每个抽屉代表一个集合，每一个苹果就可以代表一个元素，假如有n+1个元素放到n个集合中去，其中必定有一个集合里至少有两个元素”

第一抽屉原理

原理1：
把多于n个的物体放到n个抽屉里，则至少有一个抽屉里的东西不少于两件

原理2：
把多于mn(m乘n)+1（n不为0）个的物体放到n个抽屉里，则至少有一个抽屉里有不少于（m+1）的物体

原理3：
把无数还多件物体放入n个抽屉，则至少有一个抽屉里有无数个物体

第二抽屉原理

把（mn－1）个物体放入n个抽屉中，其中必有一个抽屉中至多有（m—1）个物体

0x03 整除

若整数b除以非零整数a，商为整数，且余数为零
则，b为被除数，a为除数，即a|b（“|”是整除符号），读作“a整除b”或“b能被a整除”

• a叫做b的约数（或因数）
• b叫做a的倍数
• 整除属于除尽的一种特殊情况

定理：

1. a|b，b|c，则，a|c
2. a|b，则，-a|b，a|-b，|a| | |b|
3. a|b，a|c，则，a|bx+cy
   例如：2｜10，2｜4，则2|310+54
4. a|b，b|a，则，|a| = |b|
5. 若 m≠0，a|b，则，a|m，b|m
6. 若 b≠0，a|b，则，|a| | |b|

0x04 约数

也称为因数（Divisor）
整数a除以整数b(b≠0) 除得的商正好是整数而没有余数，我们就说a能被b整除，或b能整除a
a称为b的倍数，b称为a的约数

• 一个整数的约数是有限的
• 它可以在特定情况下成为公约数

10的正约数：1、2、5、10
11的正约数：1、11

最大公约数&最小公倍数

最大公因数，也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个
a1和a2的最大公因数，记做(a1,a2)

定义一：
a1和a2是两个整数，如果d｜a1，且d｜a2，那么d为a1和a2的公约数

定理一：
(a1,a2)=(a2,a1)=(-a1,a2)=(|a1|,|a2|)

定理二：
对任意的整数x,(a1,a2)=(a1,a2,a1x)

定理三：
对任意的整数x,(a1,a2)=(a1,a2+a1x)

定理四：
aj|c(1≤j≤k)的充分必要条件是[a1,…,ak]|c
公倍数一定是最小公倍数的倍数

两个或多个整数公有的倍数叫做它们的公倍数，其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数

求约数

1. 枚举法：将两个数的因数分别一一列出，从中找出其公因数

2. ** 短除法：**短除符号就是除号倒过来。短除就是在除法中写除数的地方写两个数共有的质因数，然后落下两个数被公有质因数整除的商，之后再除，以此类推，直到结果互质为止

3. 分解质因数：将需要求最大公因数的两个数A，B分别分解质因数，再从中找出A、B公有的质因数，把这些公有的质因数相乘，即得A、B的最大公约数

4. ** 辗转相除法：**又称为欧几里得算法
   对要求最大公因数的两个数a、b，设b<a，先用b除a，得a=bq+r1(0≤r1<b）
   若r1=0，则（a，b)=b
   若r1≠0，则再用r1除b，得b=r1q+r2 (0≤r2<r1）
   若r2=0，则（a，b)=r1
   若r2≠0，则继续用r2除r1……如此循环，直到能整除为止
   其最后一个非零余数即为（a，b）

5. 更相减损术：“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。以等数约之。”
   第一步：任意给定两个正整数a、b；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步
   第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。这个数就是a、b的最大公约数
   例如：21和7，21-7=14，14-7=7，此时减数和差相等，则7为最大公因数

0x05 素数和合数

素数又称为质数（prime number）
质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数

合数（Composite number）
合数是指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数

性质：
质数的个数是无穷的

证明：
欧几里得的《几何原本》中有一个经典的证明，它使用了证明常用的方法：反证法
具体证明如下：假设质数只有有限的n个，从小到大依次排列为p1，p2，……，pn，设N=p1×p2×……×pn，那么， 是素数或者不是素数

如果N+1为素数，则N要大于p1，p2，……，pn，所以它不在那些假设的素数集合中

S1区间1——72，有素数18个，孪生素数7对
S2区间73——216，有素数27个，孪生素数7对
S3区间217——432，有素数36个，孪生素数8对
S4区间433——720，有素数45个，孪生素数7对
S5区间721——1080，有素数52个，孪生素数8对
S6区间1081——1512，素数60个，孪生素数9对
S7区间1513——2016，素数65个，孪生素数11对
S8区间2017——2592，素数72个，孪生素数12对
S9区间2593——3240，素数80个，孪生素数10对
S10区间3241——3960，素数91个，孪生素数19对
S11区间3961——4752素数92个，孪生素数17对
S12区间4752——5616素数98个，孪生素数13对
S13区间5617——6552素数108个，孪生素数14对
S14区间6553——7560素数113个，孪生素数19对
S15区间7561——8640素数116个，孪生素数14对

定理一：a>1是合数的充分必要条件
a=de，1<d<a，1<e<a

定理二：若d>1，q是可约数且d|q，则d=q
d|q指q可约除尽d，若q是可约数，则a=1或q，但是前提已经给出，d>1，则d=q

0x06 带余数除法

带余数除法也称为除数算法

设a，b是两个给定的整数，a≠0，那么，一定存在唯一一对整数q与r，满足b=qa+r，0≤r<|a|

其中q叫做不完全商，r叫做余数

推论一：
设a>0，任一整数被a除后所得的最小非负余数是且仅是0，1，…，a-1设a个数中的一个

推论二：
相邻的a个整数倍a除后，恰好取到这个a个余数，特别的，一定有有切仅有一个数被a整除

0x07 算数基本定理

算术基本定理，也称为唯一因式分解定理和素数分解定理，指出每个大于 1 的整数都可以唯一地表示为素数的乘积，直至因式的阶数

定理一：
设p是素数，p|a1a2，那么 p|a1 或 p|a2 至少有一个成立
若p|a1…an，那么 p|a1,…,p|an 至少有一个成立

References：
https://baike.baidu.com/
《初等数论》