0x01 概率论

概率论，是研究随机现象数量规律的数学分支

随机现象是相对于决定性现象而言的，在一定条件下必然发生某一结果的现象称为决定性现象，也叫做必然现象
随机现象则是指在基本条件不变的情况下，每一次试验或观察前，不能肯定会出现哪种结果，呈现出偶然性

事件的概率是衡量该事件发生的可能性的量度
虽然在一次随机试验中某个事件的发生是带有偶然性的，但那些可在相同条件下大量重复的随机试验却往往呈现出明显的数量规律，这种规律性也叫做统计规律性

样本空间

随机试验E的所有基本结果组成的集合为E的样本空间
样本空间的元素称为样本点或基本事件

• 每一个随机试验相应的有一个样本空间，样本空间的子集就是随机事件
• 由一个样本点组成的单点集，称为基本事件
• 样本空间包含所有样本点，它是自身的子集，在每次试验中它总是发生的，称为必然事件
• 空集不包括任何样本点，也作为样本空间的子集，它在每次试验中都不发生，称为不可能事件

事件间的关系

• A⊂B，则称事件B包含事件A，事件A发生的话导致事件B发生
• A⊂B且B⊂A，则A=B，称事件A与事件B相等
• A∪B = {x|x∈A 或 x∈B}，称为事件A与事件B的和事件，有些地方也叫并事件，并且当A或者B发生的时候A∪B发生

维恩图

维恩图（Venn diagram），或译Venn图、文氏图、温氏图、韦恩图
是在所谓的集合论（或者类的理论）数学分支中，在不太严格的意义下用以表示集合（或类）的一种草图

维恩图在数学事件上用的非常多，例如下图：

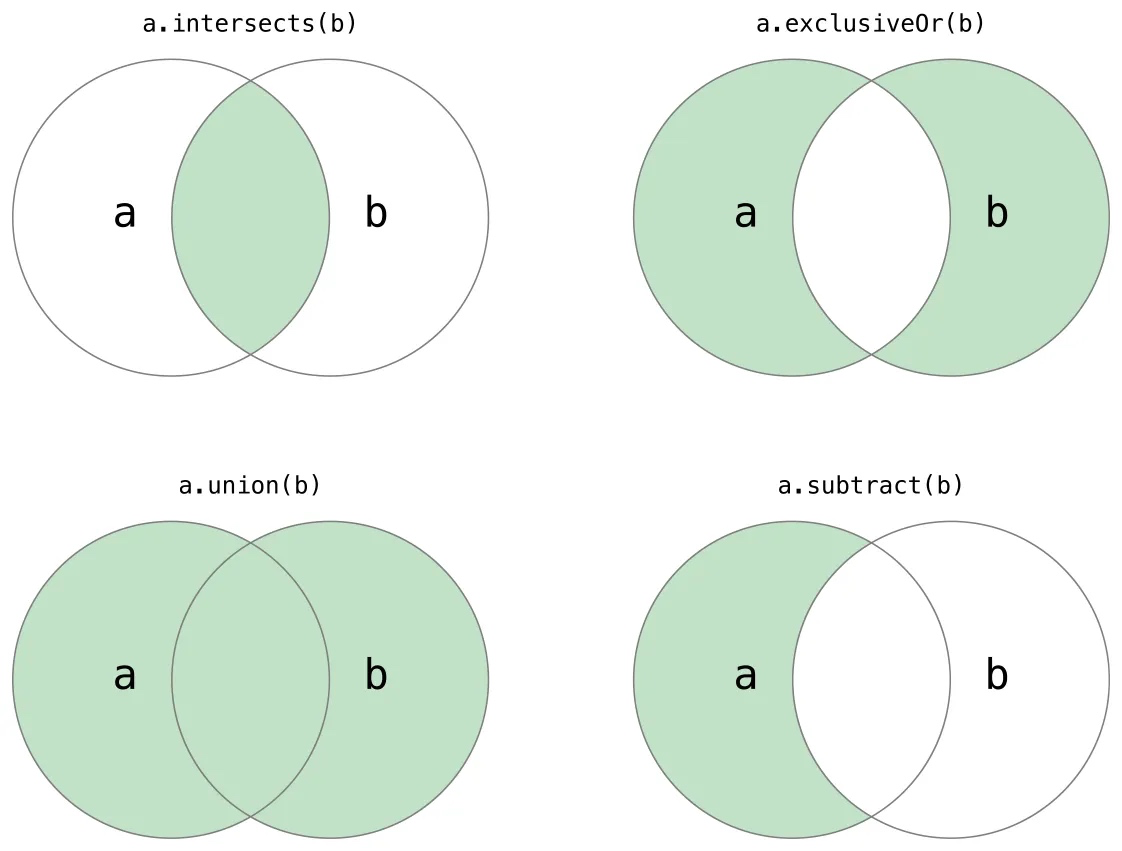
Address：http://www.wenjiangs.com/doc/dbslug-7

• intersects图：a∩b
• exclusiveOr图：a∪b-a∩b
• union图：a∪b
• subtrsct图：a-b

事件运算满足的定律：

• 交换律：A∪B=B∪A， AB=BA。
• 结合律：（A∪B）∪C=A并（B∪C）
• 分配律：（A∪B）C=（AC）∪（BC）

     （AB）∪C=（A∪C）（B∪C）

• 对偶律：A∪B的对立事件 = A的对立·B的对立
• AB的对立事件 = A的对立∪B的对立

频数&频率&概率

设想在相同的条件下，进行了n次试验，其中有a次发生了A事件，则a为频数，a/n为频率

• 频率（frequency）是单位时间内完成周期性变化的次数，是描述周期运动频繁程度的量
• 频率（probability）：反映随机事件出现的可能性大小

0x02 条件概率

条件概率是指：事件A在另外一个事件B已经发生条件下的发生概率
条件概率表示为：P（A|B），读作“在B的条件下A的概率”

条件概率可以用决策树进行计算，条件概率的谬论是假设 P(A|B) 大致等于 P(B|A)

数学家John Allen Paulos 在他的《数学盲》一书中指出医生、律师以及其他受过很好教育的非统计学家经常会犯这样的错误,这种错误可以通过用实数而不是概率来描述数据的方法来避免

基本定理

定理1

设A，B 是两个事件，且A不是不可能事件，则称![-w223]
为在事件A发生的条件下，事件B发生的条件概率，一般地，

，且它满足以下三条件：

• 非负性
• 规范性
• 可列可加性

定理2

设E 为随机试验，Ω 为样本空间，A，B 为任意两个事件，设P(A)>0，称
为在“事件A 发生”的条件下事件B 的条件概率
上述乘法公式可推广到任意有穷多个事件时的情况
设A1，A2，…An为任意n 个事件（n≥2）且
，则

定理3(全概率公式)

定义：（完备事件组/样本空间的划分）
设B1，B2，…Bn是一组事件，若

则称B1，B2，…Bn样本空间Ω的一个划分，或称为样本空间Ω 的一个完备事件组

思想：将复杂事件拆为更简单事件

定理（全概率公式）：

设事件组
是样本空间Ω 的一个划分，且P（Bi）>0（i=1，2，…n）
则对任一事件B，有

定理4(贝叶斯公式)

设B1，B2，…Bn…是一完备事件组，则对任一事件A，P（A）>0，有

事件的独立性

若：P(A∩B)=P(A)P(B)
则A，B为两个独立事件

• P(A|B)=P(A)
• P(B|A)=P(B)

事件的互斥性

若：P(A∩B) = 0
且P(A)≠0，P(B)≠0
则：

• P(A|B)=0
• P(B|A)=0

0x03 随机变量

随机变量（random variable）
表示随机试验各种结果的实值单值函数，随机事件不论与数量是否直接有关，都可以数量化，即都能用数量化的方式表达

随机事件数量化的好处是可以用数学分析的方法来研究随机现象

离散型随机变量

离散型（discrete）随机变量即在一定区间内变量取值为有限个或可数个
离散型随机变量通常依据概率质量函数（PMF）分类，（质量函数是离散随机变量在各特定取值上的概率）

常见为：
伯努利分布、二项随机变量、几何随机变量和泊松随机变量

伯努利分布

伯努利分布指的是对于随机变量X有，参数为p(0<p<1)，如果它分别以概率p和1-p取1和0为值
EX = p，DX = p(1-p)
伯努利试验成功的次数服从伯努利分布，参数p是试验成功的概率

伯努利分布是一个离散型机率分布，是N=1时二项分布的特殊情况，为纪念瑞士科学家詹姆斯·伯努利(Jacob Bernoulli 或James Bernoulli)而命名

连续型随机变量

连续型（continuous）随机变量即在一定区间内变量取值有无限个，或数值无法一一列举出来

常见为：
均匀随机变量、指数随机变量、伽马随机变量和正态随机变量

0x04 连续型随机变量

连续型随机变量是指：如果随机变量 X 的所有可能取值不可以逐个列举出来，而是取数轴上某一区间内的任一点的随机变量

对于随机变量 X，若存在一个非负的可积函数f(x)，使得对任意实数x，有

则称X为连续型随机变量
其中 f(x) 为 X 的概率分布密度函数，简称概率密度记为

0x05 分布函数

分布函数（Cumulative Distribution Function, 简称CDF）
是概率统计中重要的函数，可用分布函数的数学分析的方法来研究随机变量。

分布函数是随机变量最重要的概率特征，分布函数可以完整地描述随机变量的统计规律，并且决定随机变量的一切其他概率特征。

分布函数的性质

1. 单调不减
   

2. 有界性
   

3. 右连续性
   

部分知识来源于东北师范大学出版的《概率论与数理统计》
https://baike.baidu.com/
https://blog.csdn.net/weixin_44696542/article/details/104475158